Suites numériques - Tableurs, Calculatrices

  • Mettre en oeuvre des algorithmes permettant de calculer un terme de rang donné
  • Mettre en oeuvre des algorithmes permettant de calculer une liste de termes de la suite
  • Savoir calculer le premiers termes d'une suite à partir d'une formule récursive ou explicite
  • Représentation graphique d'une suite
Dans chaque partie, nous raisonnons sur des exemples concrets de suite. Une fonction \(f\) sera proposée dans chaque partie.

ICalcul direct sur calculatrice

Cette partie répond à la question : "comment calculer rapidement les premiers termes d'une suite à l'aide de sa calculatrice ?"

1Suite définie explicitement

On pose \(u_n = \sqrt{3 n + 2}\) pour \(n \in \mathbb{N}\).
  • Afin de calculer le terme \(u_0\) de rang \(0\) sur une calculatrice graphique, on tape
    √(3*0 + 2)
  • On peut calculer les termes suivants sans retaper toute la formule :
    TI82
    On rappelle le calcul précédent en tapant
    +
    préc
    résol
    Entrer
     , puis on remplace
    0
    par le rang désiré.

2Suite définie récursivement

Soit \((u_n)\) une suite définie récursivement pour tout \(n \geq 0\) par : $$ \left\{ \begin{array}{lll} u_{n+1} &=& \sqrt{2 u_n + 3} \\ u_0 &=& 1 \end{array} \right. $$
La méthode suivante marche sur n'importe quel type de calculatrice graphique :
On va utiliser une variable de la calculatrices
A
pour mémoriser chaque terme succéssif de la suite, en partant du premier \(u_0 = -1\) :
  • On commence par mémoriser la valeur initiale dans la variable A en tapant
    1 → A
  • Il faut calculer \(\sqrt{2 u_0 + 3}\) pour obtenir \(u_1\). De plus, on le mémorise dans la variable A :
    √(2*A+3)→A
On obtient la valeur \(u_1\), qui remplace l'ancienne valeur \(u_0\) dans la variable A.
  • Il faut calculer \(\sqrt{2 u_1 + 3}\) pour obtenir \(u_2\) et le mémoriser dans A : il n'y a qu'à taper le même calcul
    √(2*A+3)→A
Cela fonctionne car la valeur de A a changé. On obtient donc \(u_2\). Il n'y a qu'à rappeler le même calcul autant de fois que nécessaire pour calculer les premiers termes de la suite, comme le représente le shéma ci-dessous :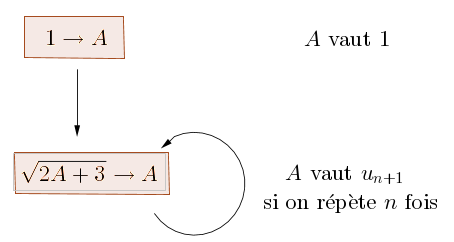

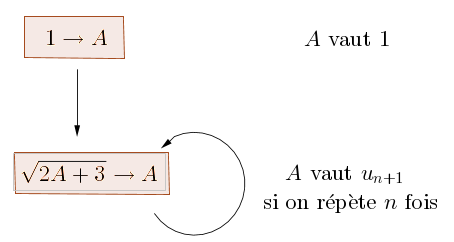
IIOutils de type tableur

En premier lieu, il faut vérifier que la calculatrice est en "mode suites" (et pas en "mode fonctions"). Il faut aller dans
quitter
mode
 , et sélectionner
Suit
ou
Seq
(français ou anglais).
Pour entrer une formule explicite, il faut aller dans
g stats
f1
f (x)
 et entrer deux informations :
  • La formule explicite à côté de
    u (n)=
  • Le rang de départ à côté de
    nMin=
    ) (0 en général)
Ci contre, on entre l'exemple suivant :
\(u_n = \frac{1}{n}\) pour tout \(n \geq 1\)
Pour
n
, taper
échanger
X,T,Θ,n
Pour entrer une formule récursive, il faut aller dans
g stats
f1
f (x)
 et entrer trois informations :
  • La formule récursive à côté de
    u (n)=
  • Le rang de départ à côté de
    nMin=
    ) (0 en général)
  • La valeur de départ (\(u_0\) en génral) à côté de
    u (nMin)
Ci contre, on entre l'exemple suivant :
\( \left\{ \begin{array}{lll} u_{n+1}&=&2 u_n \\ u_0&=&1 \end{array} \right. \)
Pour
u
, taper
+
un
O
7
Attention, la ti82 décale les indices :
  • \(u_{n+1}\) s'écrit
    u (n)
  • \(u_{n}\) s'écrit
    u (n-1)
On peut lire les valeurs dans le tableur
+
table
f5
graphe
 . 		$$ u_n = \frac{1}{n}$$ $$ \left\{ \begin{array}{lll} u_{n+1}&=&2 u_n \\ u_0&=&1 \end{array} \right. $$
  • Il faudra penserà remettre la calculatrice en "mode fonction" en sélectionnant
    Fonc
    dans
    quitter
    mode
     pour un chapitre sur les fonctions.
  • Le tableur peut être paramétré dans déf table
    +
    déf table
    f2
    fenêtre
     . On peut choisir le point de départ de la table dans
    DébutTbl
    et laisser le calcul manuel (
    Demande
    ) ou automatique (
    Auto
    ). Le mode manuel est utile pour choisir directement une valeur de rang élevé comme \(u_{100}\) sans faire défiler toutes les valeurs précédentes.

IIITracer un nuage de points

Tout d'abord, la calculatrice doit être en mode suite, et la formule (explicite ou récursive) doit être rentrée dans
g stats
f1
f (x)
 .
On va tracer le nuage de points de la suite définie explicitement par \(u_n = \frac{1}{n}\) pour \(1\leq n \leq 10\)
Avant de tracer les points, il faut paramétrer la fenêtre dans
déf table
f2
fenêtre
  • nMin
    correspond à l'indice du premier point à tracer et
    nMax
    au dernier
  • Xmin
    et
    Xmax
    sont les bornes de l'axe des abscisses. On peut mettre les mêmes valeurs que pour
    nMin
    et
    nMax
    , ou un peu plus large.
  • Ymin
    et
    Ymax
    sont les bornes de l'axe des ordonnées. Il vaut les choisir par rapport à la plus grande valeur et la plus petite valeur des \(u_n\).
Ici comme on trace les 10 premières valeurs de \(u_n=\frac{1}{n}\), on choisit :

\(nMin = 1\), \(nMax = 10\), \(Xmin = 0\), \(Xmax = 10\), \(Ymin = 0\), \(Ymax = 1\)

Il n'y a plus qu'à appuyer sur
table
f5
graphe
 pour tracer le nuage de points.

IVAlgorithmes

1Calcul du k-ième terme

2Calcul des premiers termes dans une liste